Just before summer holidays began, a friend of mine reached out and shared this question with me. It was an Argand Diagrams question taken from the Dr Frost Maths website.
(Swipe or click+arrow keys to scroll through the workings, it may take a few seconds to load)
\begin{equation}\mathrm{A\ complex\ number\ z\ is\ represented\ by\ the\ point\ P\ on\ an\ Argand\ Diagram.}\\ \mathrm{Given\ that\ }arg\left(\frac{z-6i}{z-3i}\right)=\frac{\pi}{3}\\\\ \\ \mathrm{The\ sketch\ of\ the\ locus\ of\ P\ as\ z\ varies\ is\ shown\ below.}\\\\ \\ \mathrm{Find\ the \ exact\ maximum\ value\ of\ } \left|z\right|.\ \mathrm{(5 \ marks ) }\end{equation}
It didn’t look too difficult at first, being only 5 marks. But what we did not know that the question required Y13 knowledge of polar coordinates (Core Pure 2) as well as the exact value answer, so this meant estimations were not allowed. We were stumped for a long time.
It took me overnight to find a (creative?) solution using whatever I had already learnt, but it was well worth it in the end.
Let’s start:
\begin{equation}arg\left(\frac{z-6i}{z-3i}\right)=\frac{\pi}{3}\\\\ \mathrm{Therefore} \frac{\pi}{3}=arg\left(z-6i\right)-arg\left(z-3i\right)\\\\\end{equation}
We know that the difference between the argument of a complex number z from 6i and 3i is equal to pi/3 radians.
Now, what? My Y12 knowledge takes me as far as here. It’s time to delve deeper.
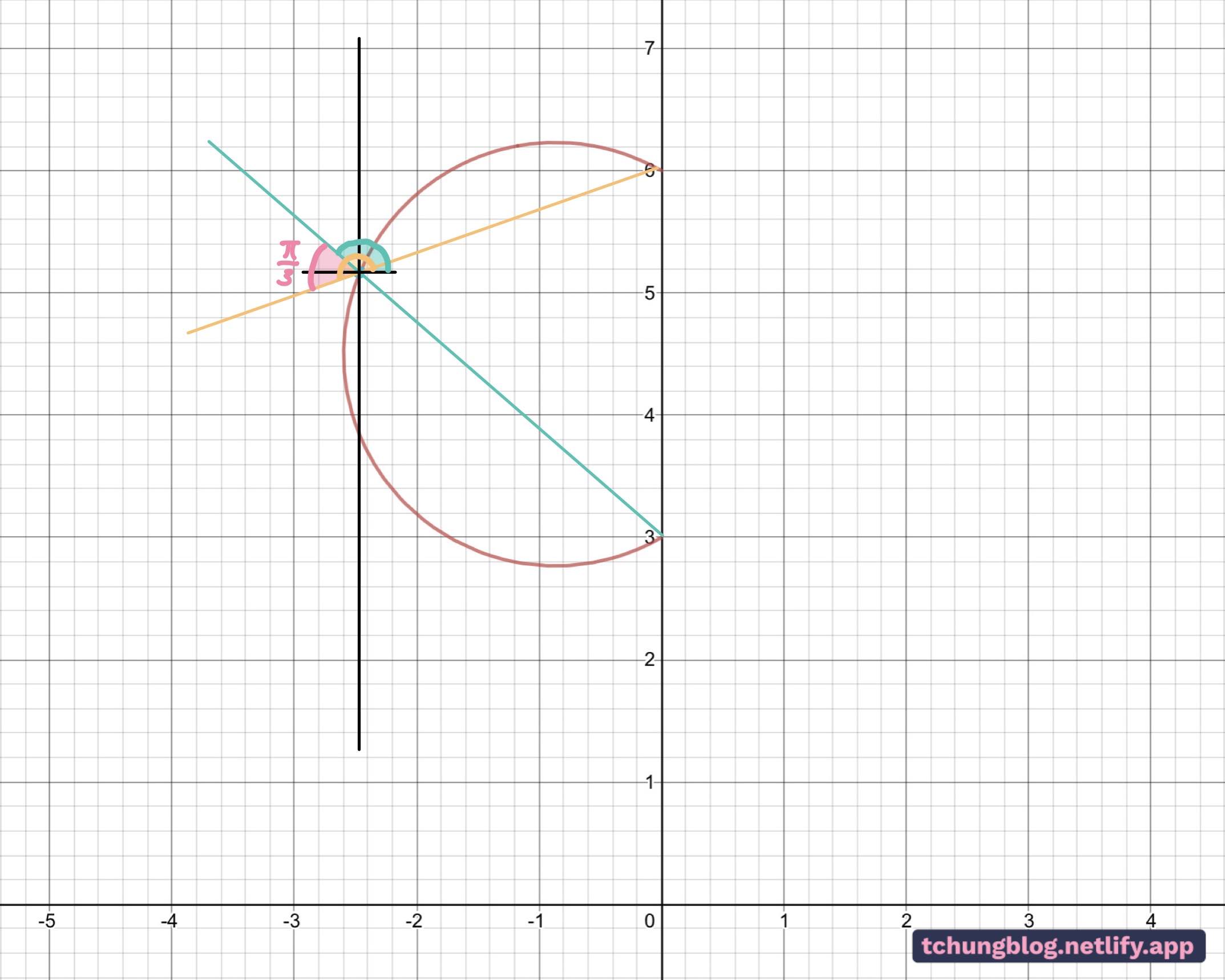
FIGURE 1
Looking at Figure 1, I’ve chosen a point on the locus and drawn argument lines from 6i and 3i to the point and highlighted the angles for clarity. Note that these lines intersect creating an acute angle of pi/3.
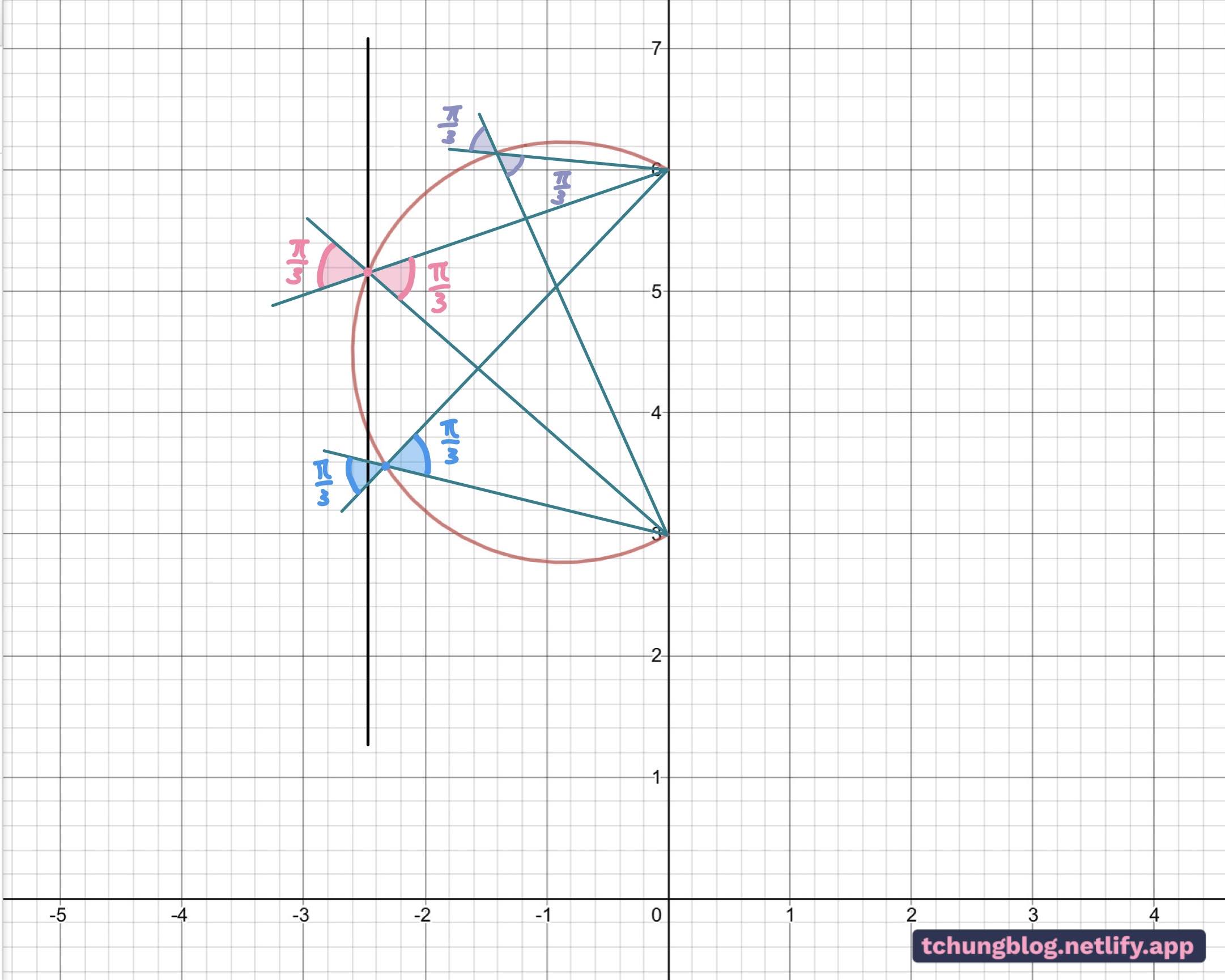
FIGURE 2
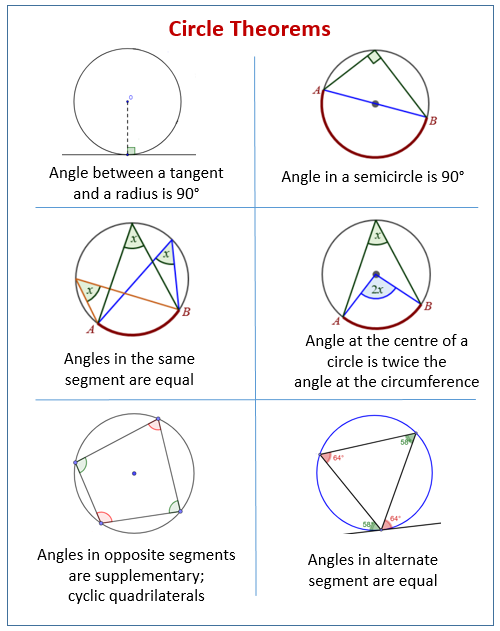
I’ve drawn more lines like shown in Fig 2. The opposite angles formed by two straight lines are the same. Do you see a pattern? (This is the circle theorem taught in IGCSEs.) We’ve proved this ellipse is really just a circle, because of the angles in the same segment are equal to one another.
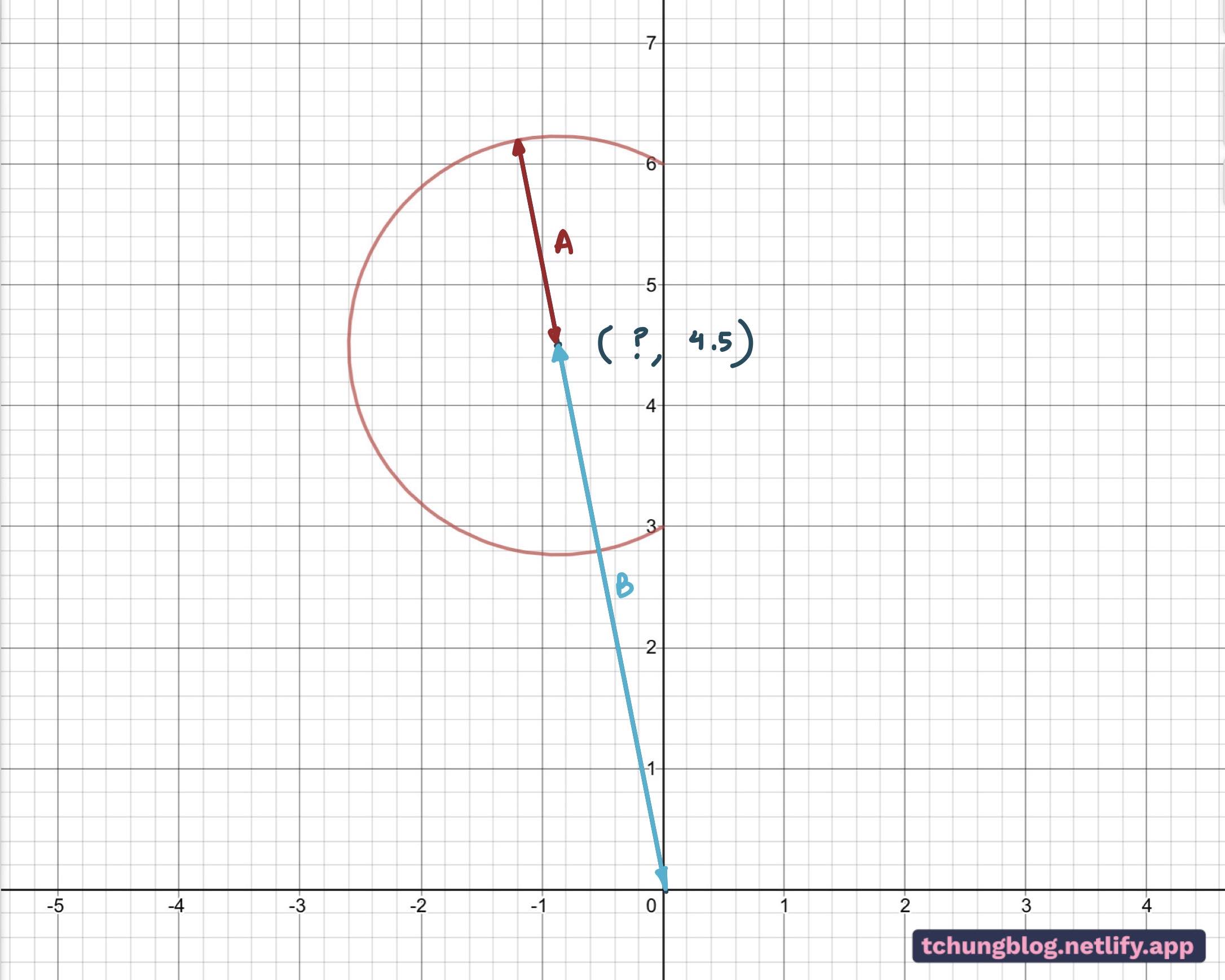
FIGURE 3
Knowing the shape is a circle, finding the largest value of |z| is easy, as shown in Figure 3.
Find the distance from origin to the centre of the circle (A), and add the radius of the circle (B). to get |z|.
This measured distance must pass through the centre of the circle because it contains the diameter, the longest possible chord/distance between two points on a circumference. The centre should have a cartesian y-coordinate of 4.5, as it is between 6 and 3, as shown in Fig 3.
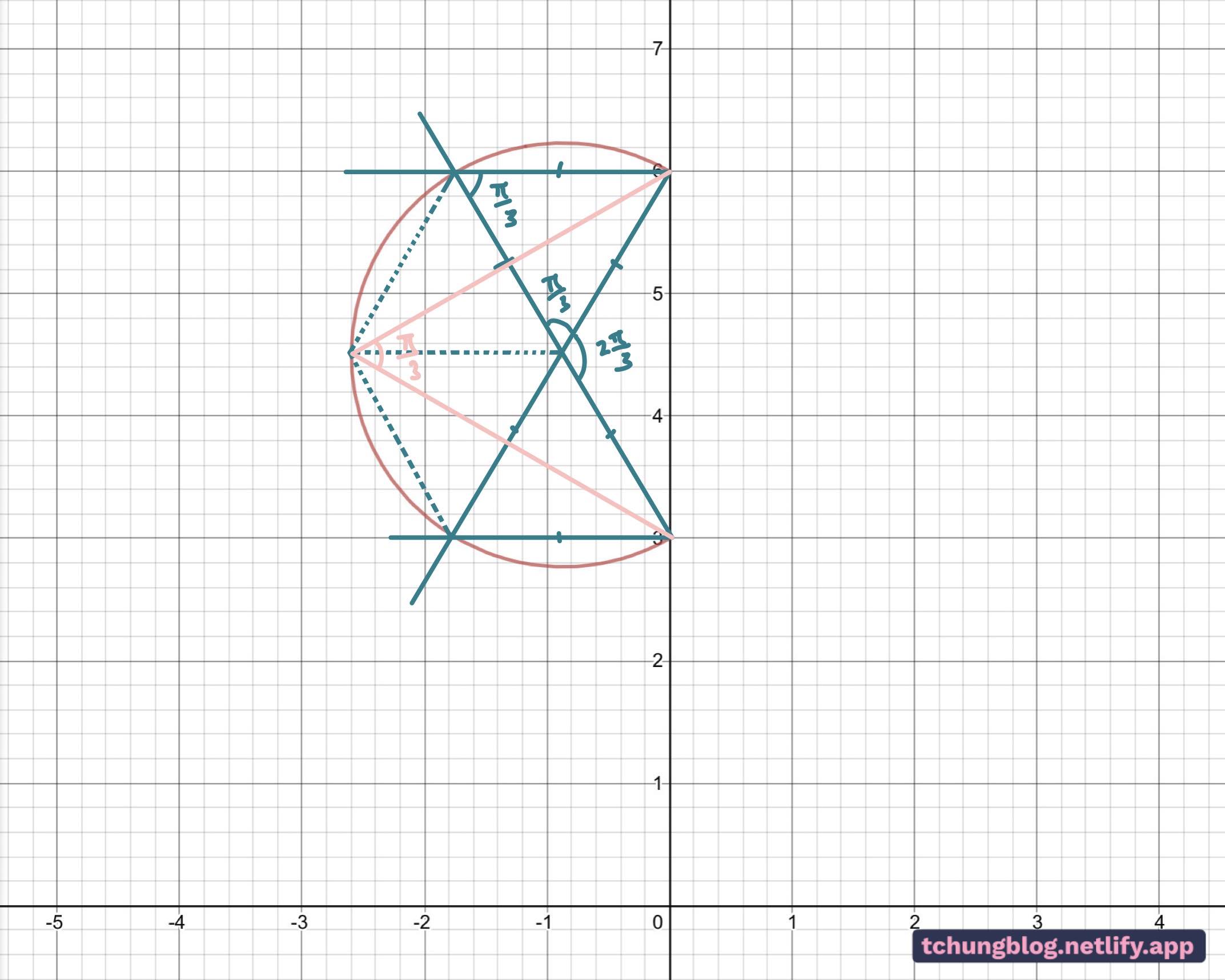
FIGURE 4
I’ve redrawn the lines again in Figure 4, revealing the very geometrically-pleasing properties of the pi/3 radians angle. I picked points that would form equilateral triangles in a hexagon shape. We’ve now worked out the angle of the isosceles triangle in Figure 5.
*Can you spot another circle rule in place here? The answer will be at the bottom of the post.
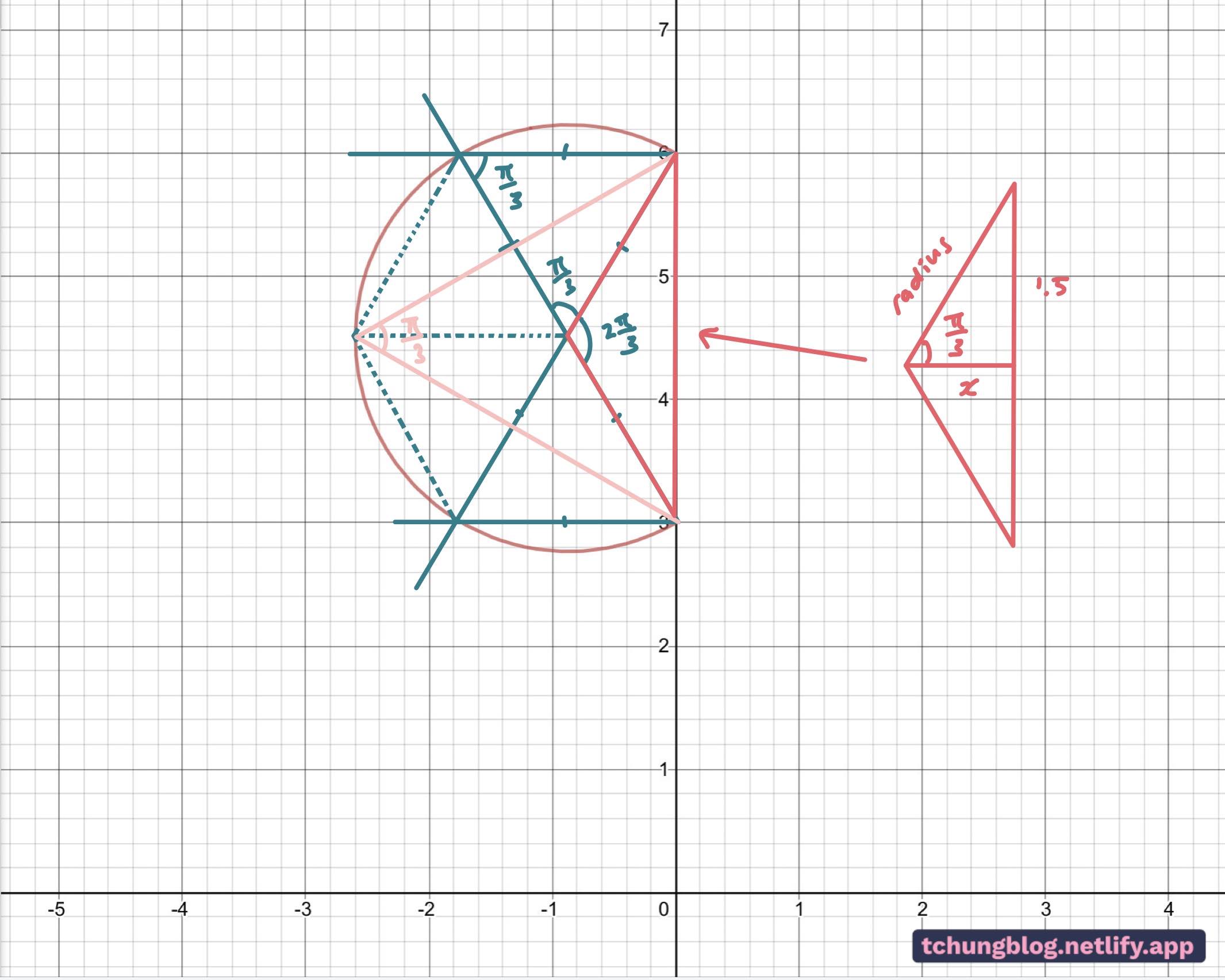
FIGURE 5
Fig 5: The radius and the centre of the circle can easily be calculated with easy trigonometry, which at this point, is mere peanuts compared to the very difficult start of this question.
\begin{equation}\sin\left(\frac{\pi}{3}\right)=\frac{1.5}{\mathrm{radius}}\\\\\frac{\sqrt{3}}{2}=\frac{1.5}{\mathrm{radius}}\\\\ \mathrm{radius}\ =\ \sqrt{3}\end{equation}
\begin{equation}\\ \therefore Length\ A\ =\ \sqrt{3}\\\\\tan\frac{\pi}{3}=\frac{1.5}{x}\\\\\sqrt{3}=\frac{1.5}{x}\\\\x=\frac{\sqrt{3}}{2}\\\\ \mathrm{So\ coordinates\ of\ the\ centre\ are}\ \left(-\frac{\sqrt{3}}{2},4.5\right)\\\end{equation}
Now, all is left is the addition of lengths A and B, to get our result in Figure 6:
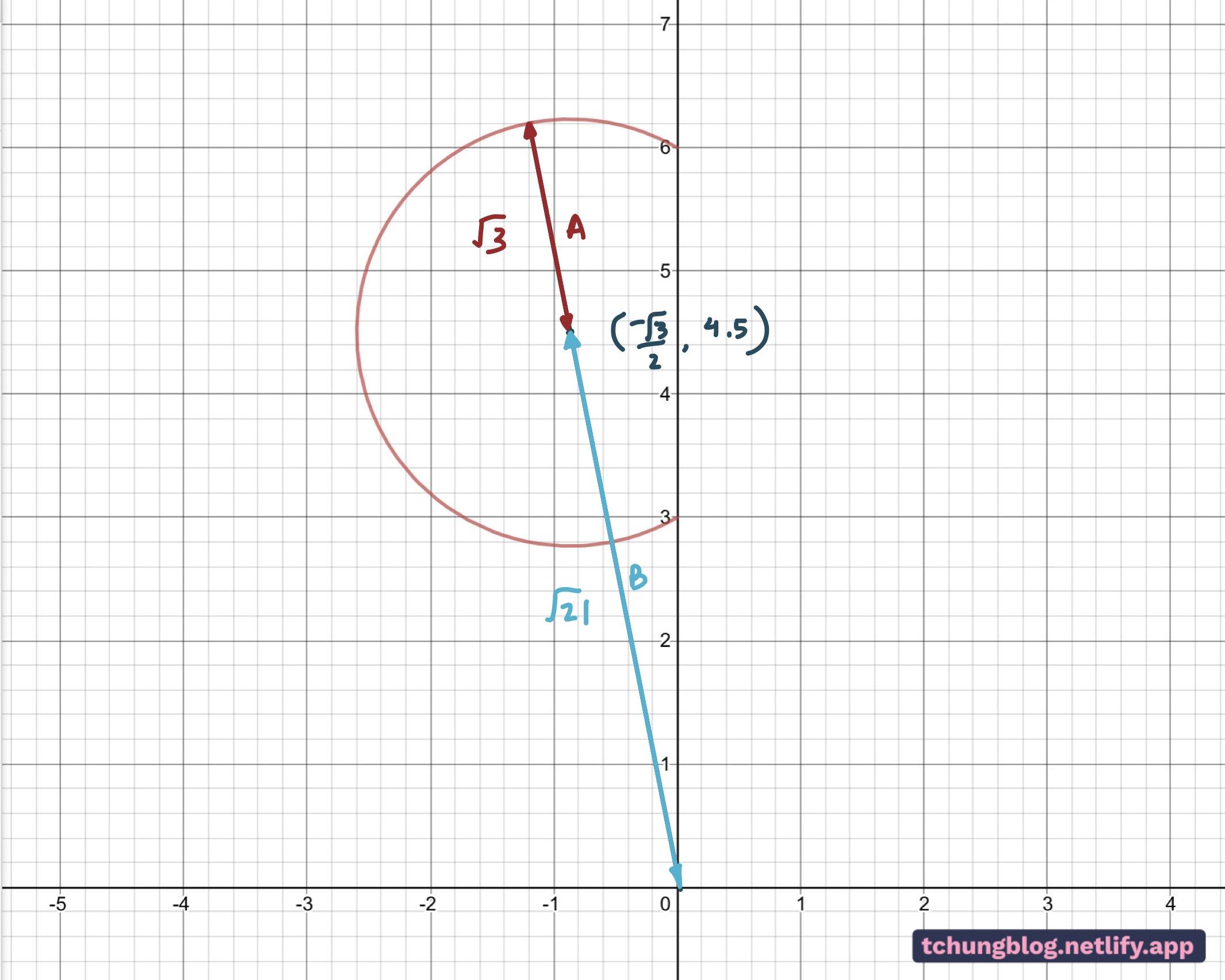
FIGURE 6
\begin{equation}\mathrm{Length}\ B\ =\ \sqrt{\left(\frac{\sqrt{3}}{2}\right)^{2}+\left(4.5\right)^{2}}\\\\=\sqrt{21}\\\\ \mathrm{\therefore\ Length} \ A\ +\ \mathrm{Length} \ B\\\\=\sqrt{21}+\sqrt{3}\end{equation}
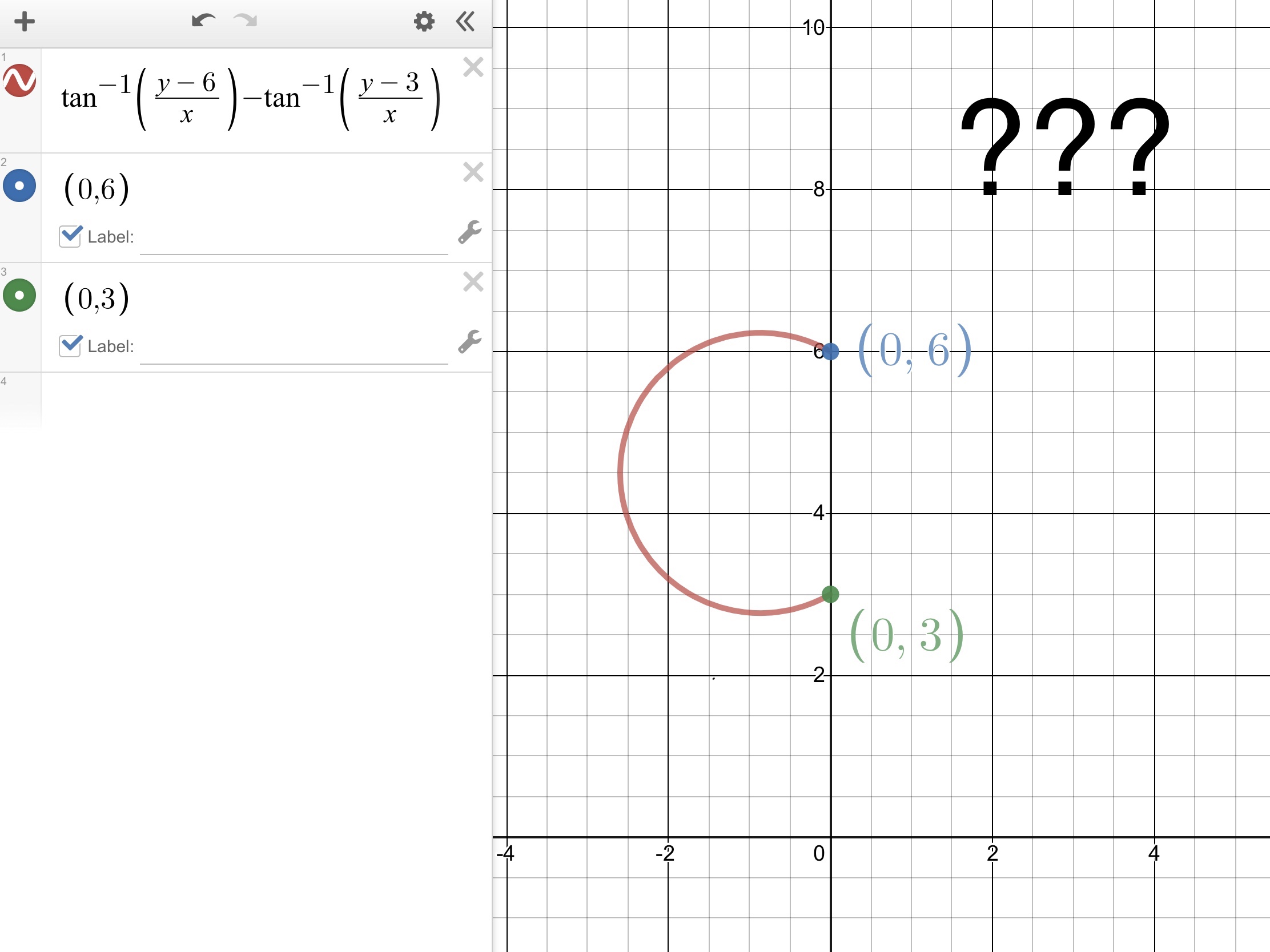
You’re probably wondering how I reverse engineered the graph for this blog post. This is how I got to the answer:
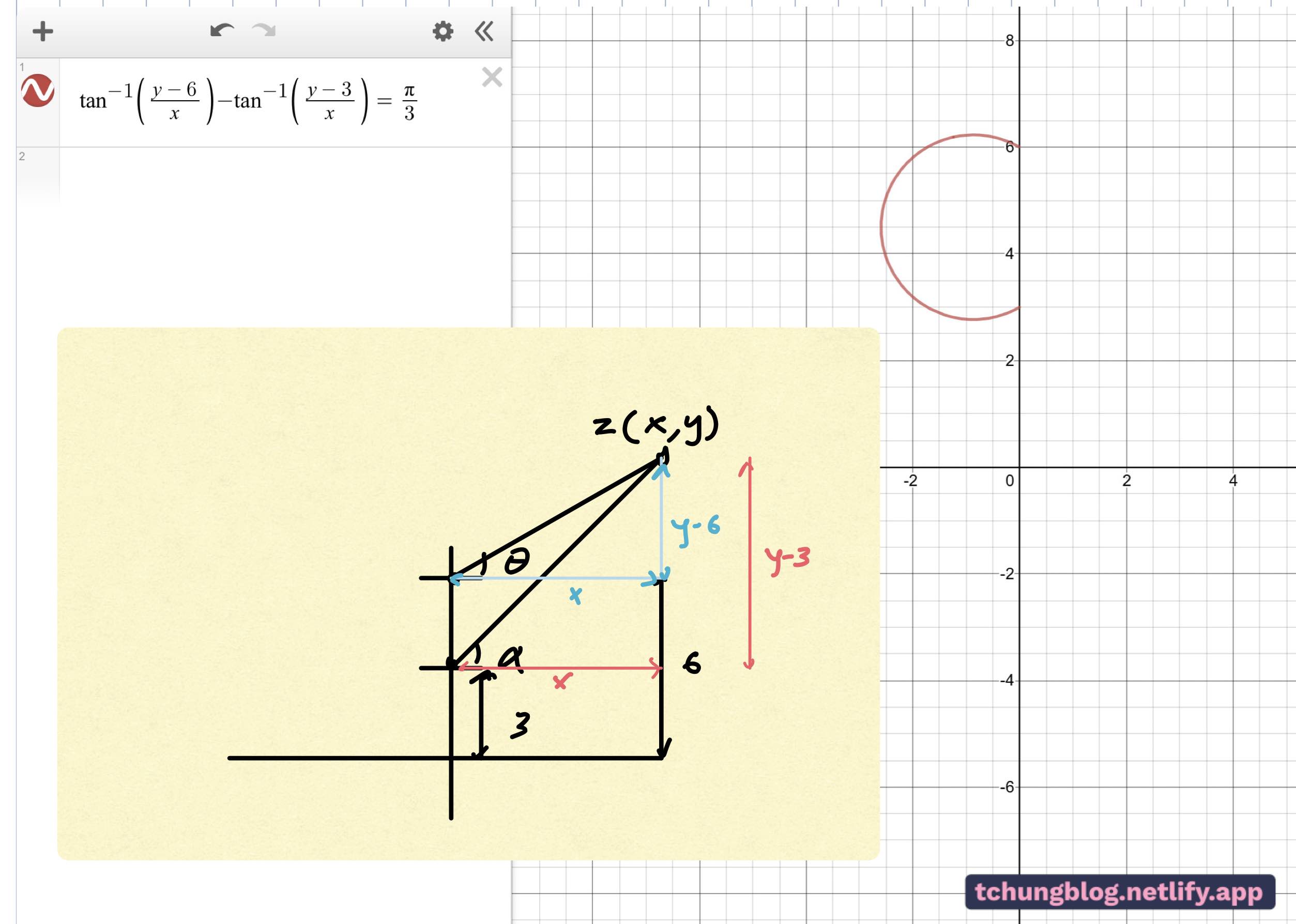
\begin{equation}\mathrm{Must\ find\ a\ point\ Z\ where} \ \ \ \theta-\alpha\ =\ \frac{\pi}{3}\\\\\\\tan^{-1}\left(\frac{y-6}{x}\right)-\tan^{-1}\left(\frac{y-3}{x}\right)=\frac{\pi}{3}\ \end{equation}
And that concludes it for this question! I did learn a lot of problem-solving skills from this one. This question ought to be worth more than 5 marks ;)
*Answer: The angle at a centre of a circle is twice the angle at the circumference (Picture from https://www.onlinemathlearning.com/)