Foreword: This post has been edited under the advice of my Mathematics teacher for better clarity and rigor. The URL of this page calls this work a ‘proof’, however after much thought, the more accurate term is ‘derivation’.

Last term, we learned about vectors in Core Pure Maths. I was curious on how the formula was derived, so after some experimentation, I used IGCSE-Level trigonometry to get to the answer.

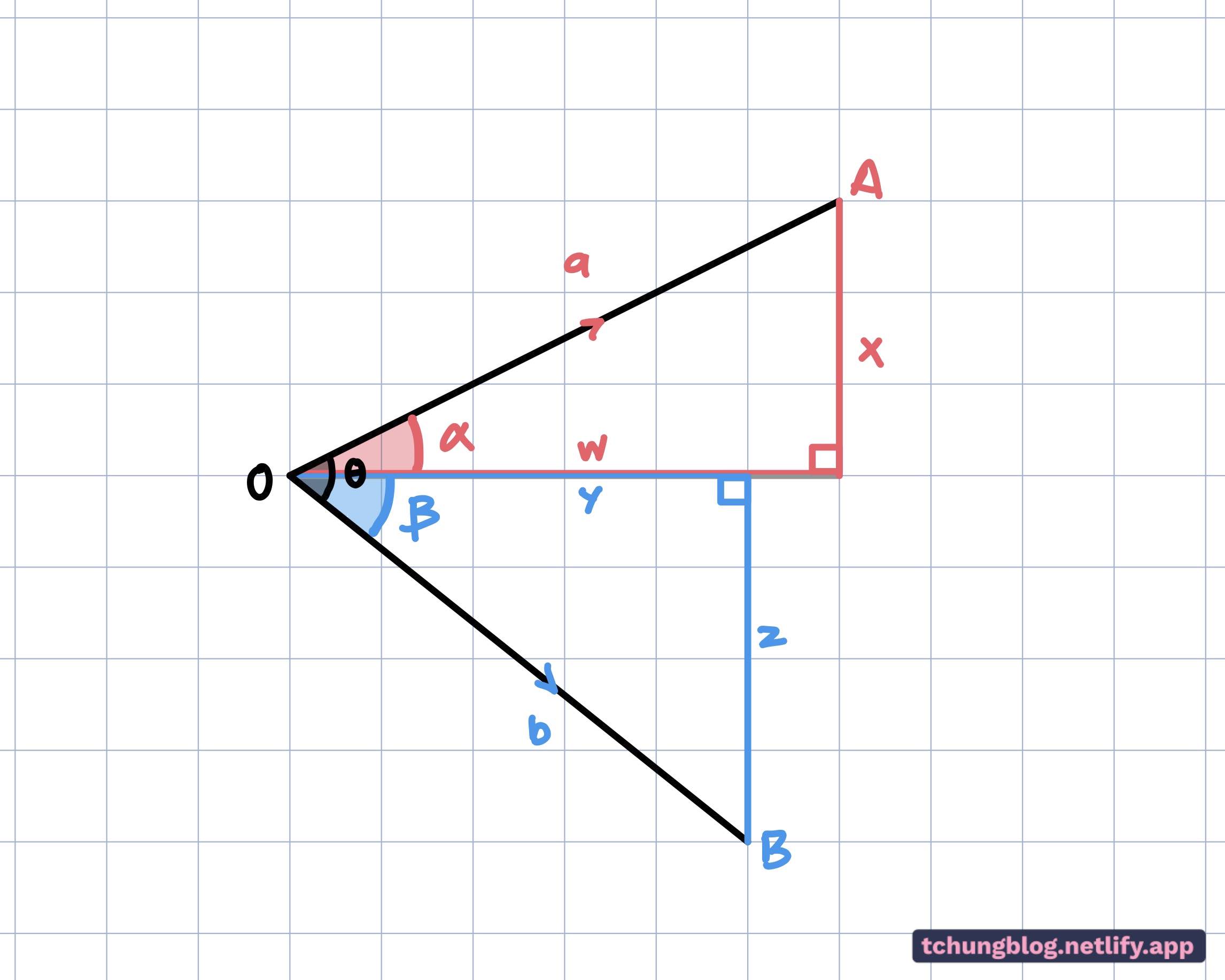
FIGURE 1:

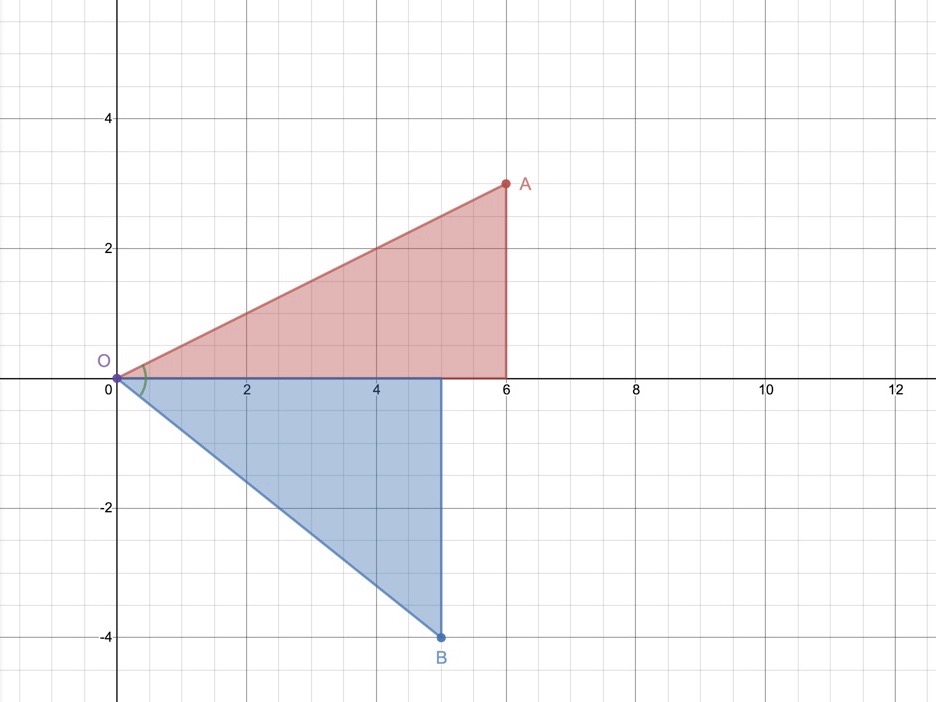
Figure 1 shows two 2-D vectors, |OA| = a, and |OB| = b. Both vectors are at an angle θ. (Swipe or click+arrow keys to scroll through the workings, it may take a few seconds to load)

Method 1: Cosine rule\begin{equation} \mathrm{Using\ the\ cos\ rule\ for\ Figure\ 1:}\\\left|OA\right|^{2}+\left|OB\right|^{2}-2\left|OA\right|\left|OB\right|\cos\theta=\left|AB\right|^{2}\\\left|OA\right|^{2}+\left|OB\right|^{2}-\left|AB\right|^{2}=2\left|OA\right|\left|OB\right|\cos\theta\ \ \ \to\mathrm{Equation\ [1]\ } \\~\\ \mathrm{Consider \ the\ LHS:} \\2\left|OA\right|\left|OB\right|\cos\theta\ \\=w^{2}+y^{2}+x^{2}+z^{2}-\left(x+z\right)^{2}-\left(w-y\right)^{2}\\=w^{2}+x^{2}+y^{2}+z^{2}-\left(x^{2}+2zx+z^{2}\right)-\left(w^{2}-2wy+z^{2}\right)\\=2wy-2zx\\~\\ \mathrm{Consider\ the\ dot\ product\ }\\ \vec{a}^{\,}=\begin{pmatrix}w\\x\end{pmatrix}\ and\ \vec{b}^{\,}=\begin{pmatrix}y\\-z\end{pmatrix} \\ \vec{a}^{\,} \cdot \vec{b}^{\,} \\= \begin{pmatrix}w\\x\end{pmatrix}\ \cdot \begin{pmatrix}y\\-z\end{pmatrix}\ \\= wy \ -\ zx \\~\\ \therefore\ \mathrm{Equation\ [1]\ becomes: }\ \\wy-zx=\left|A\right|\left|B\right|\cos\theta\\\frac{\left(wy-zx\right)}{\left|OA\right|\left|OB\right|}=\cos\theta\\\frac{a\cdot b}{\left|OA\right|\left|OB\right|}=\cos\theta\end{equation}

After finishing Core Pure 1’s Trigonometry chapters, I used some new trigonometry formulas recently learned to simplify the derivation.

Method 2: Cosine Addition Rule\begin{equation} \cos\left(a+b\right)=\cos a\cos b-\sin a\sin b \\\\ \\\\=\left(\frac{w}{\sqrt{w^{2}+x^{2}}}\times\frac{y}{\sqrt{y^{2}+z^{2}}}\right)-\left(\frac{x}{\sqrt{w^{2}+x^{2}}}\times\frac{z}{\sqrt{y^{2}+z^{2}}}\right)\\\\ \\\\=\frac{wy-xz}{\sqrt{w^{2}+x^{2}}\sqrt{y^{2}+z^{2}}}\\\\ \\\\=\frac{a\cdot b}{\left|OA\right|\left|OB\right|} \end{equation}

It’s interesting to see the cosine addition formula reduces the number of lines of working. Also, note how the left hand side of the equation slowly takes the shape of the dot product.

I haven’t looked much into the use case of the dot product, although 3Blue1Brown has a video about it here. At 6:27, the video shows that a dot product of two vectors is simply mapping one onto the other. I will have to look further into this, and also the cross product, which was removed from the exam specification for some reason…

Using the cosine addition simplifies the formula for 2-dimensional vectors. What about 3-dimensional vectors? (Prepare for a large chunk of working)

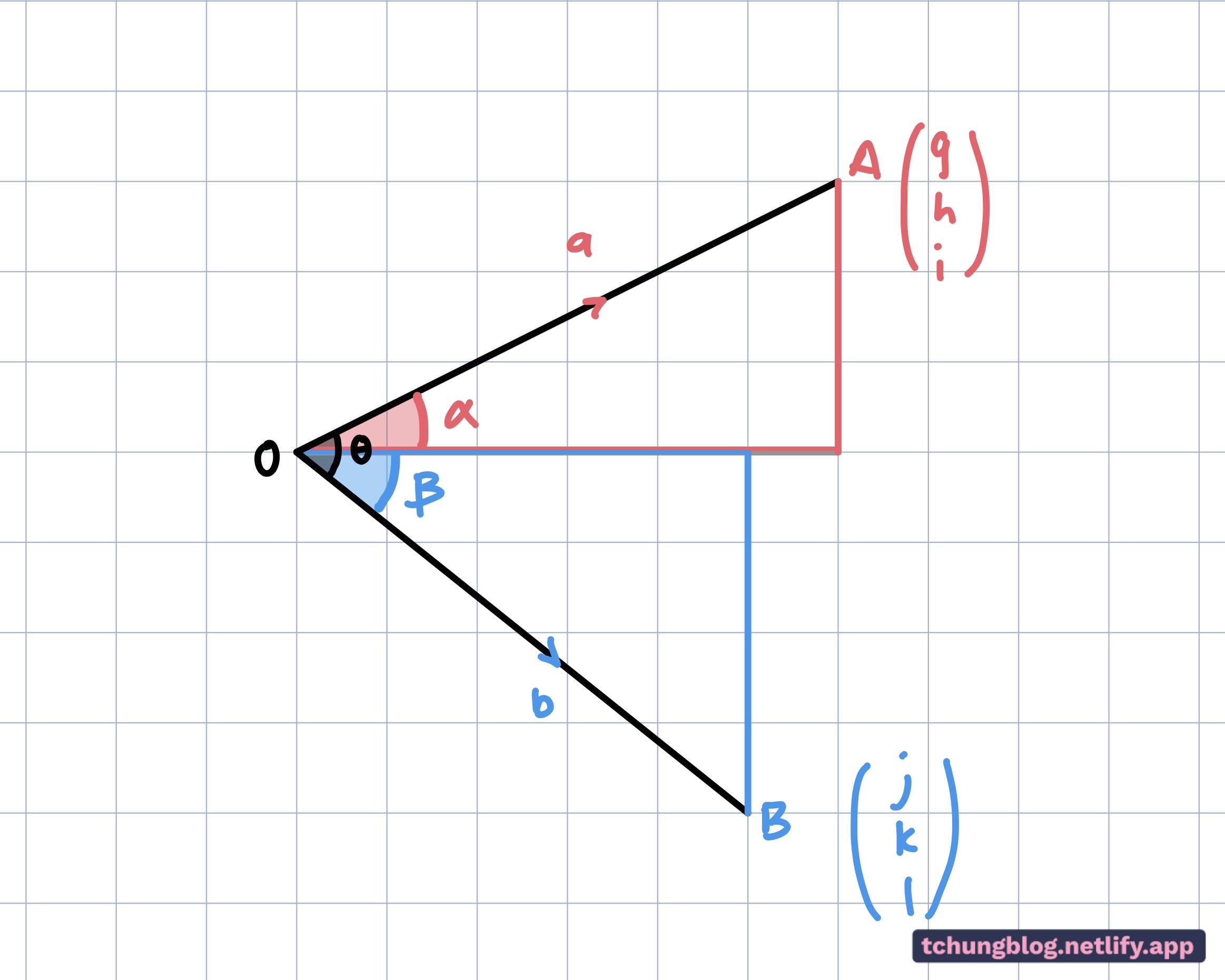FIGURE 2

Figure 2 is similar to Figure 1 , but now vectors a and b have a component of (g,h,i) and (j,k,l) respectively. I’ve used a style similar to Method 1 to work things out:

\begin{equation}\vec{a}^{\,}=\begin{pmatrix}g\\h\\i\end{pmatrix}\ and\ \vec{b}^{\,}=\begin{pmatrix}j\\k\\l\end{pmatrix}\\ \mathrm{Using\ the\ cos\ rule:}\\\left|\vec{a}^{\,}\right|^{2}+\left|\vec{b}^{\,}\right|^{2}-2\left|\vec{a}^{\,}\right|\left|\vec{b}^{\,}\right|\cos\theta=\left|-\vec{a}^{\,}+\vec{b}^{\,}\right|^{2}\\\left|\vec{a}^{\,}\right|^{2}+\left|\vec{b}^{\,}\right|^{2}-\left|-\vec{a}^{\,}+\vec{b}^{\,}\right|^{2}=2\left|\vec{a}^{\,}\right|\left|\vec{b}^{\,}\right|\cos\theta\\\left|\vec{a}^{\,}\right|^{2}+\left|\vec{b}^{\,}\right|^{2}-\begin{vmatrix}-g+j\\-h+k\\-i+l\end{vmatrix}^{2}=2\left|\vec{a}^{\,}\right|\left|\vec{b}^{\,}\right|\cos\theta\\g^{2}+h^{2}+i^{2}+j^{2}+k^{2}+l^{2}-\left(\left(j-g\right)^{2}+\left(k-h\right)^{2}+\left(l-i\right)^{2}\right)=2\left|\vec{a}^{\,}\right|\left|\vec{b}^{\,}\right|\cos\theta\\g^{2}+h^{2}+i^{2}+j^{2}+k^{2}+l^{2}-j^{2}-g^{2}-k^{2}-h^{2}-l^{2}-i^{2}+2jg+2kh+2li=2\left|\vec{a}^{\,}\right|\left|\vec{b}^{\,}\right|\cos\theta\\2gj+2hk+2il=2\left|\vec{a}^{\,}\right|\left|\vec{b}^{\,}\right|\cos\theta\\gj+hj+il=\left|\vec{a}^{\,}\right|\left|\vec{b}^{\,}\right|\cos\theta\\\begin{pmatrix}g\\h\\i\end{pmatrix}\cdot\begin{pmatrix}j\\k\\l\end{pmatrix}=\left|\vec{a}^{\,}\right|\left|\vec{b}^{\,}\right|\cos\theta\\\frac{\vec{a}^{\,} \cdot \vec{b}^{\,}}{\left|\vec{a}^{\,}\right|\left|\vec{b}^{\,}\right|}=\cos\theta\end{equation}

Again, note how the left hand side of the equation slowly develops into the dot product.

Well, that concludes a little bit of derivation for today. Stay tuned for more maths posts!