Search Problems are a core part of AI. Whenever you intend to compute something, there can be many outcomes, but only a select few are the ones you are looking for. Real life examples include Google Maps trying to find the shortest path between two places, solving puzzles like tic-tac-toe, etc.

Before we go on, here are some definitions:

Agent: An entity that perceives its environment and acts upon it

State: A configuration of the agent and its environment.

Actions: Choices that can be made in a state

Transition Model: The result of performing a certain, possible action in a state.

State Space: The set of all the states reachable from its initial state by any sequence of actions.

Goal Test: Determine if the given state is a goal state, or the state that we are looking for.

Path Cost: Numerical cost of a given path.

Node: A data structure that keeps track of a:

• a state
• a parent (node that generated this node)
• an action (applied to parent to reach this node)
• a path cost (from initial state to node)

The Algorithm

You can visualise nodes as being interconnected together in a decentralised net. The idea is, you want to start with the initial node or initial state, and find the shortest path to the goal state. Then pick adjacent nodes that aren’t explored and see if they’re the one that is the goal state.

This is how the algorithm works, in more detail:

1. Start with a frontier that contains the initial state.
2. Start with an empty explored set.
3. Repeat:
   1. If the frontier is empty, there is no solution
   2. Remove a node from the frontier.
   3. If the node is the goal state, return the solution.
   4. Add the node to the explored set.
   5. Expand the node, adding more nodes to the frontier if they are not in the explored set.

Let’s start with an example: Consider this environment of nodes; we want to get from A to G.

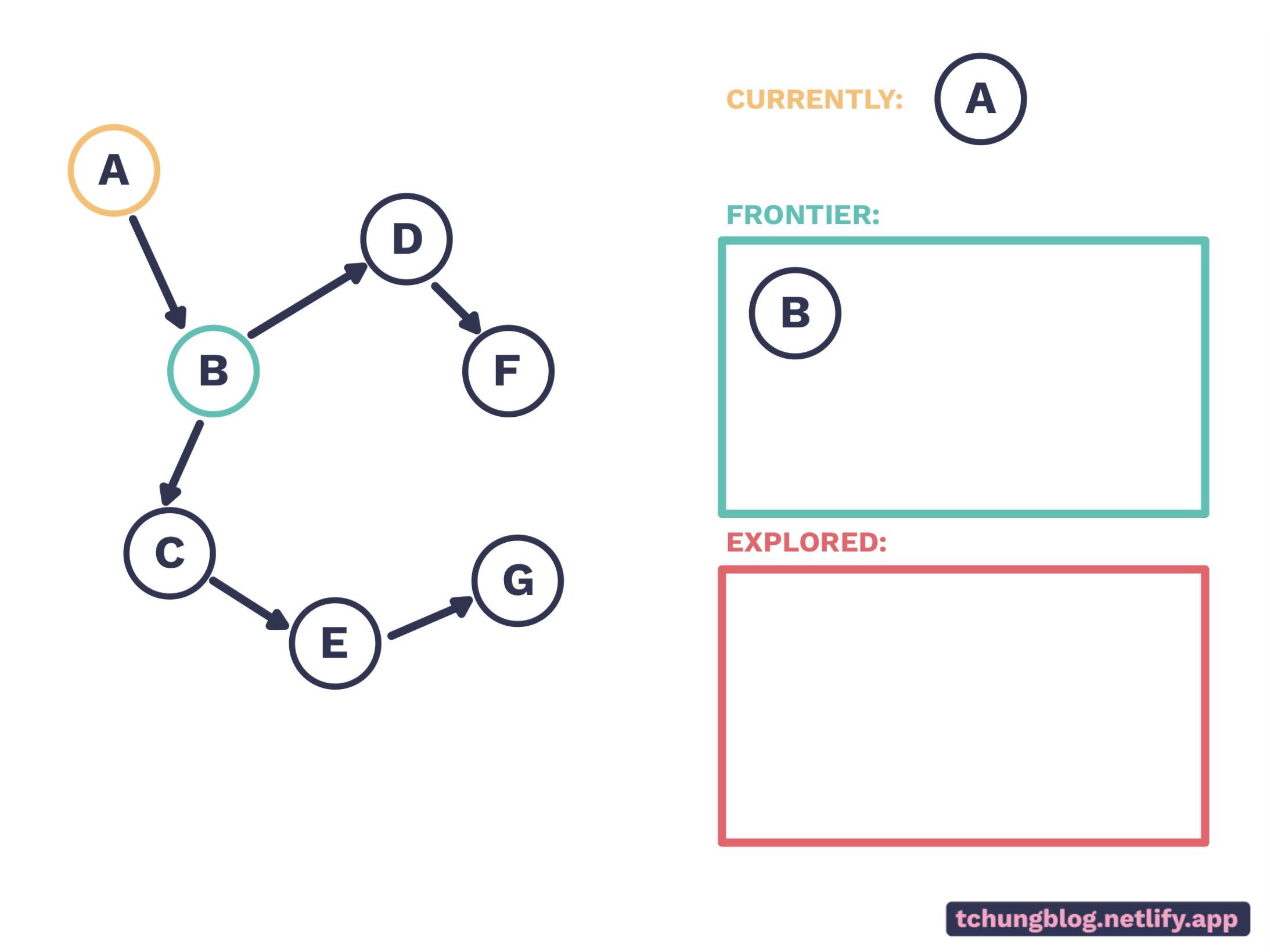
A is our initial node, and B is in our frontier. We now remove B from the frontier…

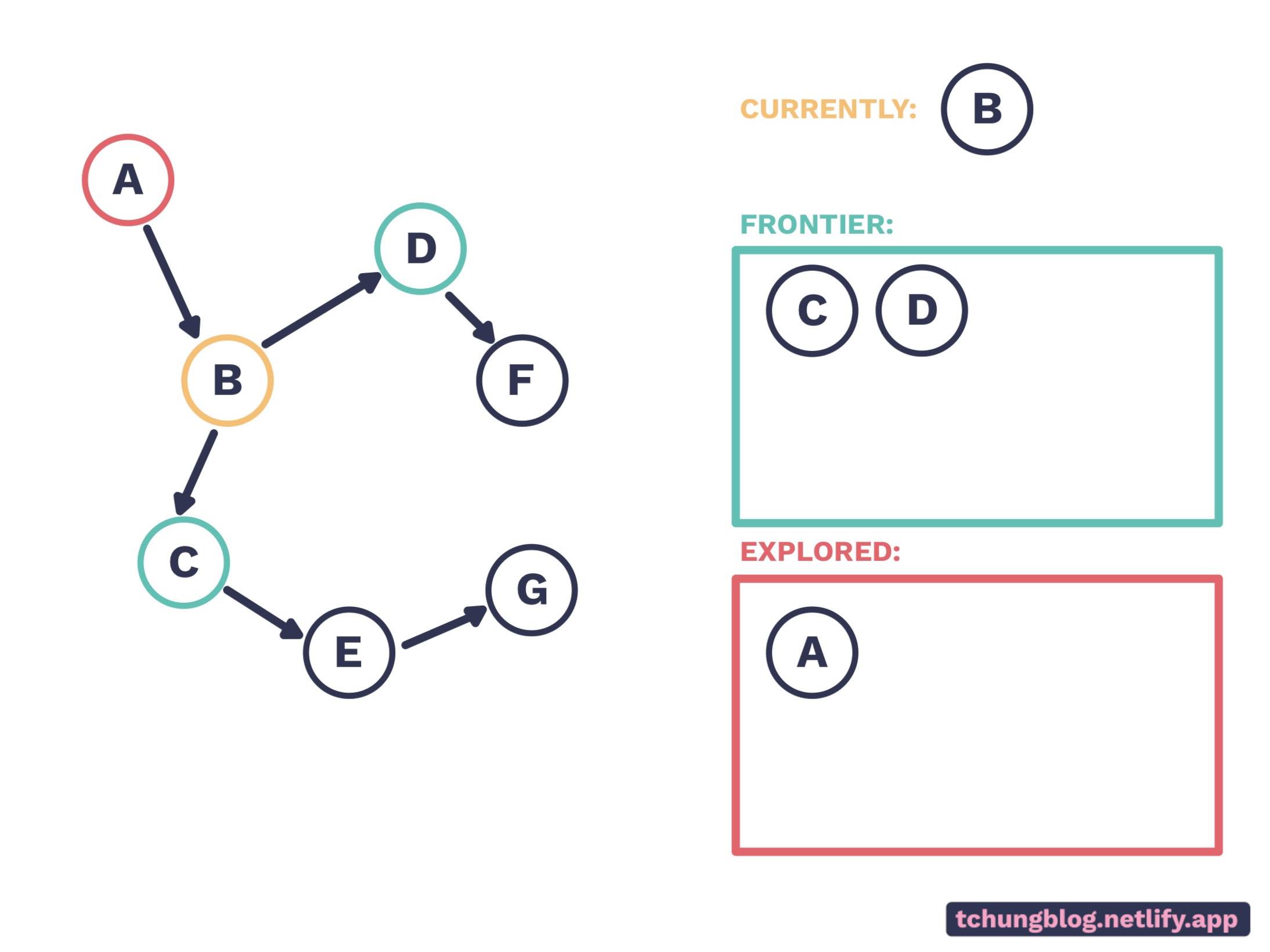
And get C and D as our new frontier. We are not in G yet, so choose D from the frontier. Note that we pick the most recent node added in the frontier: this action is known as last-in-first-out.

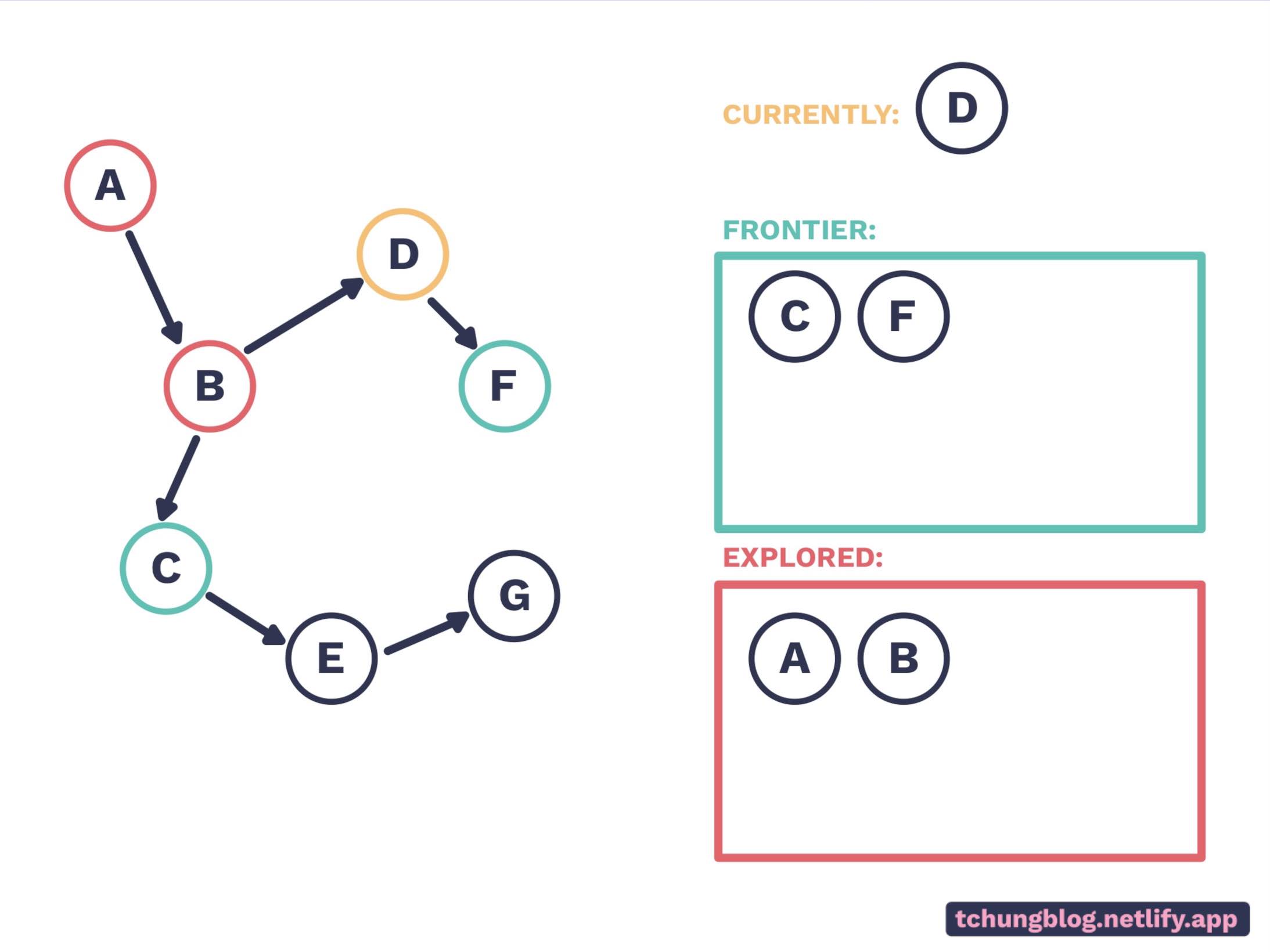
D is removed from the frontier, and C and F is added to the frontier.

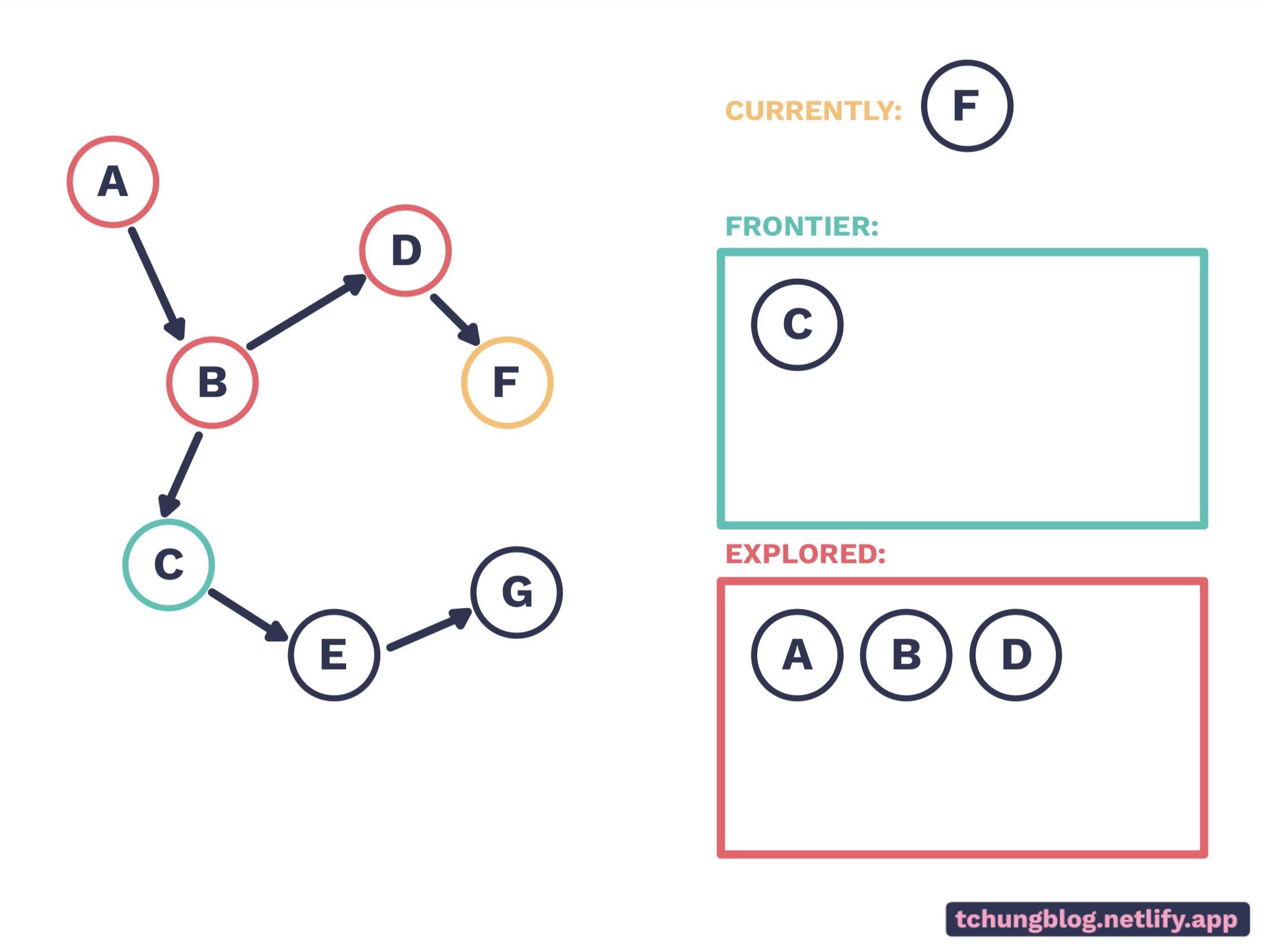
F is a dead end. Since C is left in the frontier, we’ll go there.

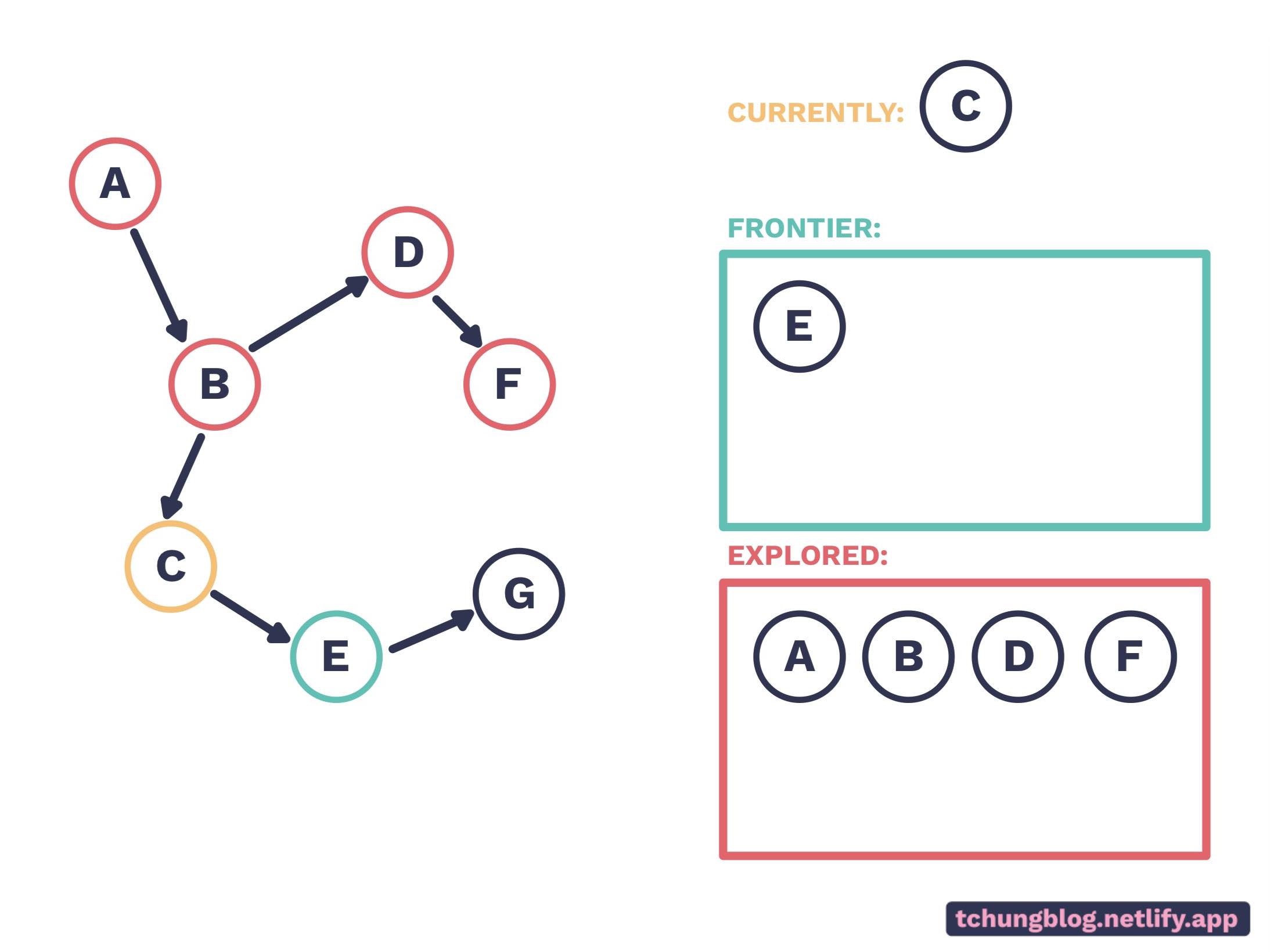
E is next in the frontier.

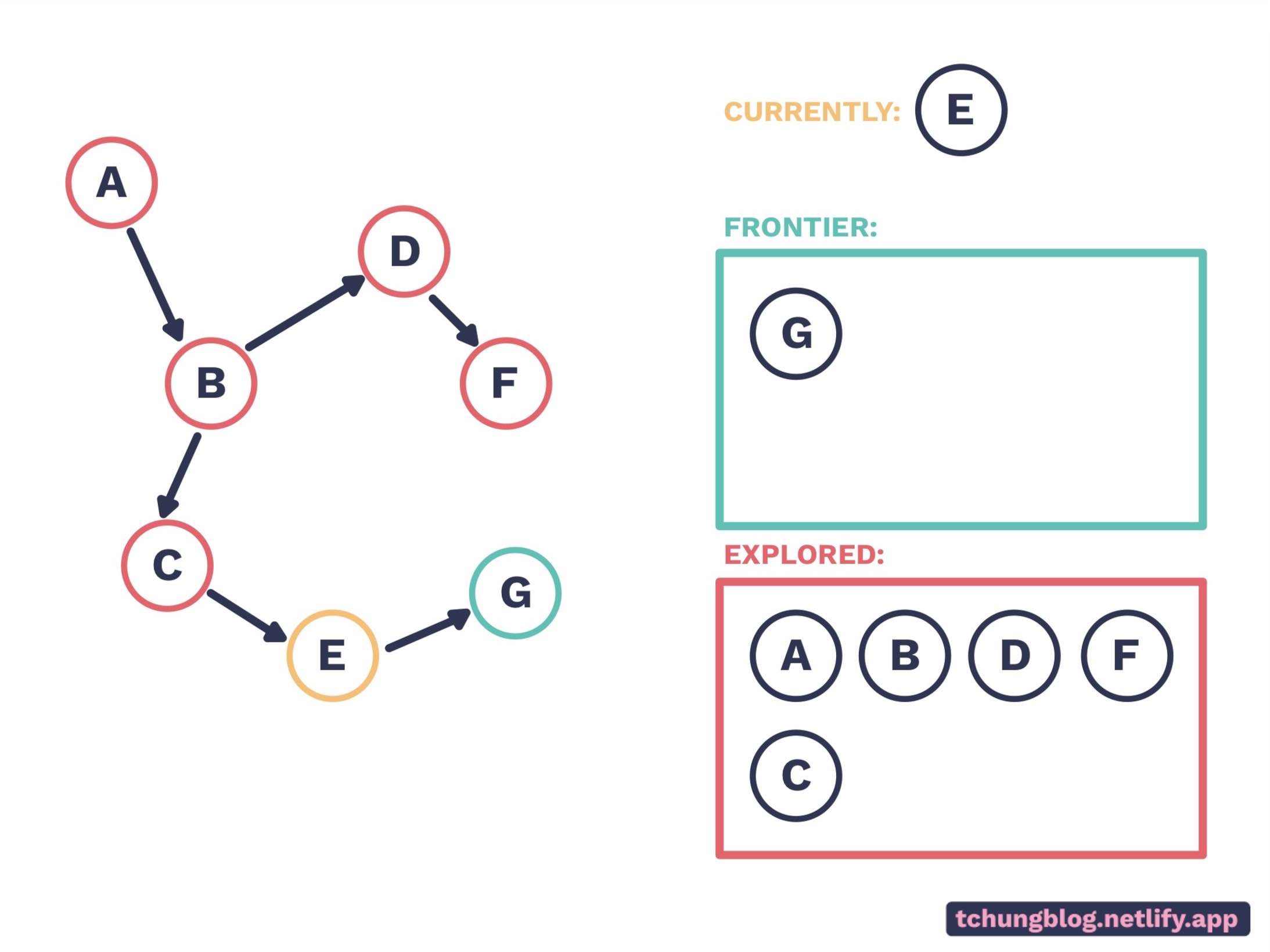
Which leaves us with G…

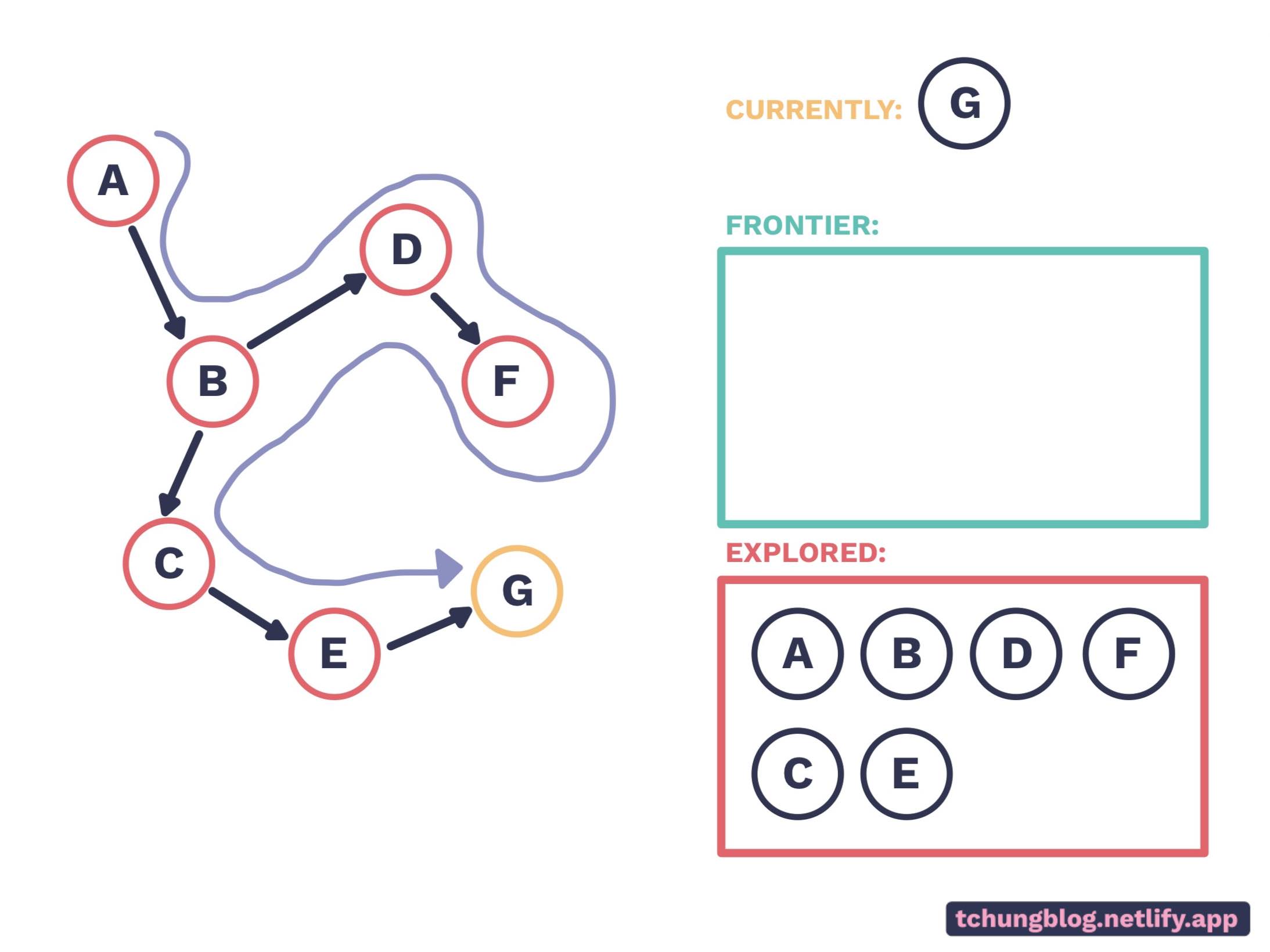
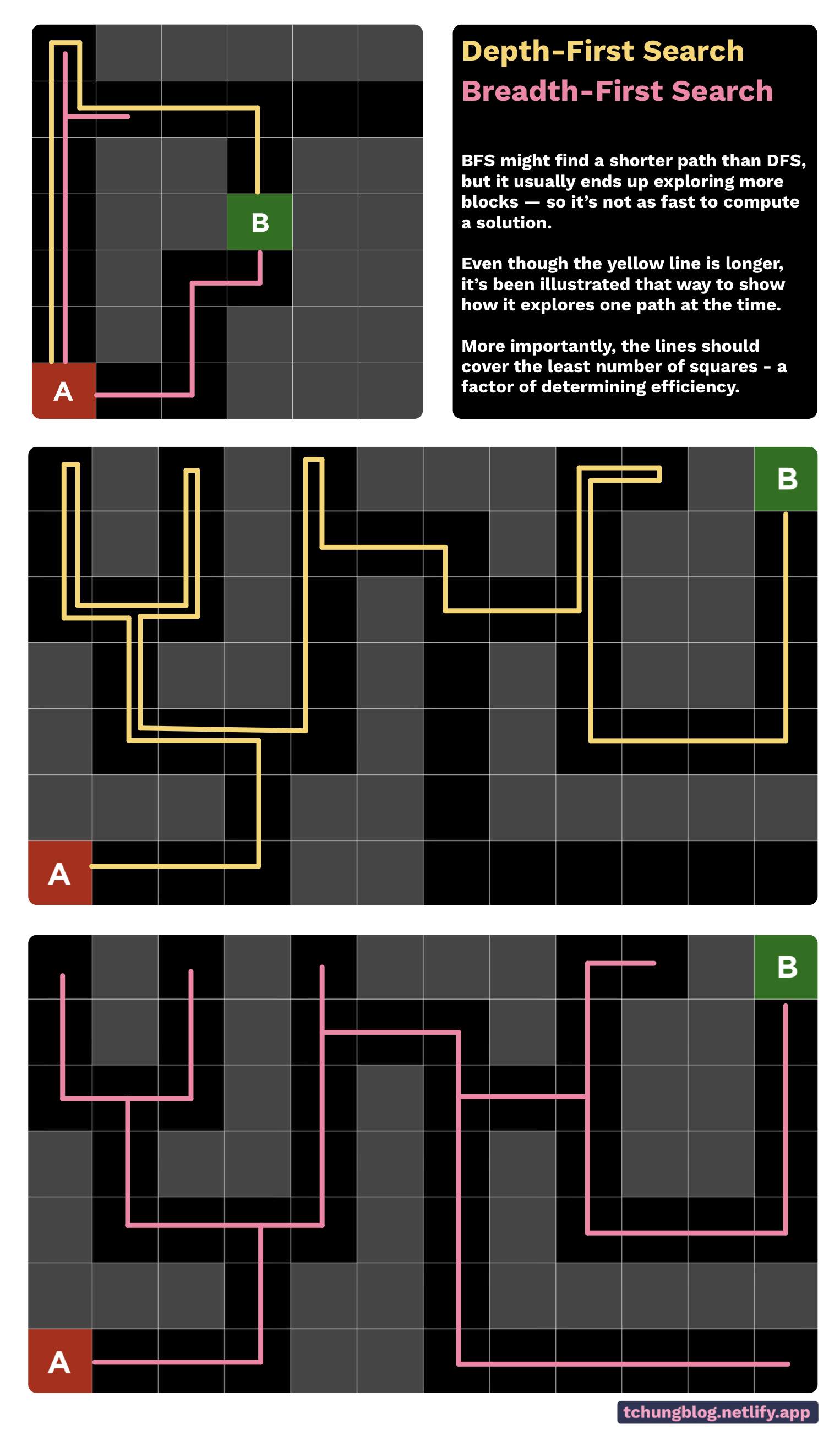
And we have reached G! If G wasn’t our goal node, this algorithm would end because its frontier is empty. Note that the algorithm explores as far as it can until it reaches a dead end, then goes back to its last fork and tries another path from there. This is also known as depth-first-search (DFS).

Another variation of this method is the breadth-first-search (BFS) , that uses a first-in-last-out method. It will branch out at every fork and explore each fork at an equal pace. Here is an example of a solving a maze using DFS and BFS: